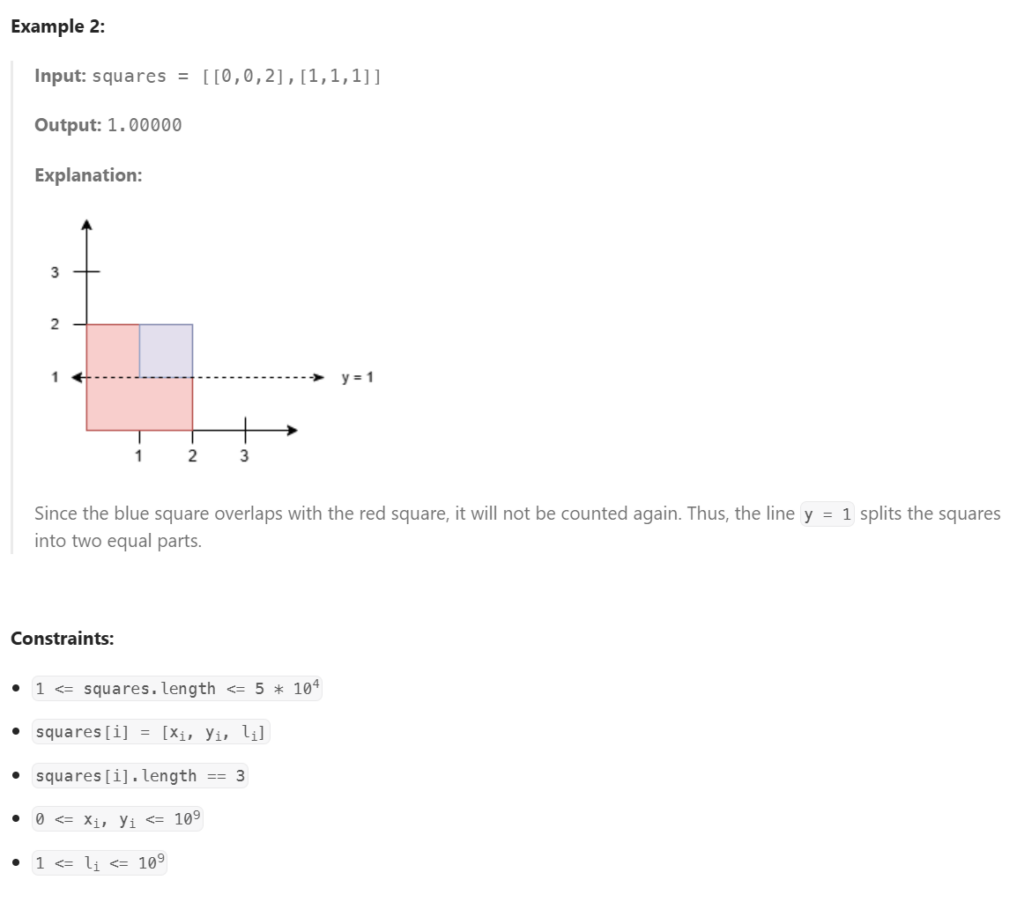
https://leetcode.com/problems/separate-squares-ii

from typing import List, Tuple
from bisect import bisect_left
class Solution:
def update(self, idx: int, l: int, r: int, ql: int, qr: int, delta: int,
xs: List[int], cnt: List[int], seg: List[float]) -> None:
# If the query interval [ql, qr) does not intersect the current node interval [l, r)
if qr <= l or r <= ql:
return
# If the current node interval is fully within the query interval
if ql <= l and r <= qr:
cnt[idx] += delta
else:
mid = (l + r) // 2
self.update(idx * 2, l, mid, ql, qr, delta, xs, cnt, seg)
self.update(idx * 2 + 1, mid, r, ql, qr, delta, xs, cnt, seg)
# Update the segment tree node value based on the count
if cnt[idx] > 0:
seg[idx] = xs[r] - xs[l]
else:
if r - l == 1:
seg[idx] = 0.0
else:
seg[idx] = seg[idx * 2] + seg[idx * 2 + 1]
def separateSquares(self, squares: List[List[int]]) -> float:
# Define an Event as a tuple: (y, type, x1, x2)
# type = 1 means a square starts (bottom edge), type = -1 means it ends (top edge)
events = []
xs = []
# Build events and record x-coordinates
for x, y, l in squares:
x2 = x + l
y2 = y + l
events.append((float(y), 1, x, x2)) # bottom edge event
events.append((float(y2), -1, x, x2)) # top edge event
xs.append(x)
xs.append(x2)
# Remove duplicate x values and sort them
xs = sorted(set(xs))
# Sort events by y-coordinate
events.sort(key=lambda e: e[0])
m = len(xs)
cnt = [0] * (4 * m)
seg = [0.0] * (4 * m)
totalArea = 0.0
prev_y = events[0][0]
segments: List[Tuple[float, float, float]] = [] # List of tuples: (y_start, y_end, union_length)
nEvents = len(events)
i = 0
# Process events in a sweep-line fashion
while i < nEvents:
cur_y = events[i][0]
# If there is a vertical gap, accumulate the area in that segment
if cur_y > prev_y:
height = cur_y - prev_y
unionLength = seg[1] # The union length is stored at the root of the segment tree
segments.append((prev_y, cur_y, unionLength))
totalArea += unionLength * height
prev_y = cur_y
# Process all events at the same y-coordinate
while i < nEvents and events[i][0] == cur_y:
y, typ, x1, x2 = events[i]
# Find the indices for x1 and x2 in the sorted xs array using bisect_left
ql = bisect_left(xs, x1)
qr = bisect_left(xs, x2)
self.update(1, 0, m, ql, qr, typ, xs, cnt, seg)
i += 1
# Now, find the y-coordinate that splits the area into two equal halves.
target = totalArea / 2.0
cum = 0.0
for seg_info in segments:
y_start, y_end, union_len = seg_info
segArea = union_len * (y_end - y_start)
if cum + segArea >= target:
if union_len == 0:
return y_start
remain = target - cum
# The additional y needed within the current segment
delta_y = remain / union_len
ans = y_start + delta_y
return ans
cum += segArea
return prev_y # Fallback in case all segments are processed