You are given an integer side, representing the edge length of a square with corners at (0, 0), (0, side), (side, 0), and (side, side) on a Cartesian plane.
You are also given a positive integer k and a 2D integer array points, where points[i] = [xi, yi] represents the coordinate of a point lying on the boundary of the square.
You need to select k elements among points such that the minimum Manhattan distance between any two points is maximized.
Return the maximum possible minimum Manhattan distance between the selected k points.
The Manhattan Distance between two cells (xi, yi) and (xj, yj) is |xi - xj| + |yi - yj|.
Example 1:
Input: side = 2, points = [[0,2],[2,0],[2,2],[0,0]], k = 4
Output: 2
Explanation:
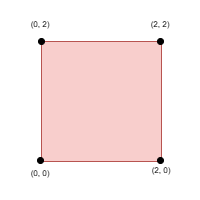
Select all four points.
Example 2:
Input: side = 2, points = [[0,0],[1,2],[2,0],[2,2],[2,1]], k = 4
Output: 1
Explanation:
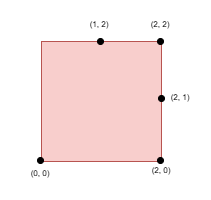
Select the points (0, 0), (2, 0), (2, 2), and (2, 1).
Example 3:
Input: side = 2, points = [[0,0],[0,1],[0,2],[1,2],[2,0],[2,2],[2,1]], k = 5
Output: 1
Explanation:
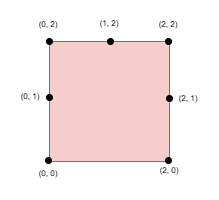
Select the points (0, 0), (0, 1), (0, 2), (1, 2), and (2, 2).
Constraints:
1 <= side <= 1094 <= points.length <= min(4 * side, 15 * 103)points[i] == [xi, yi]- The input is generated such that:
points[i]lies on the boundary of the square.- All
points[i]are unique.
4 <= k <= min(25, points.length)
from bisect import bisect_left
from typing import List
class Solution:
def mapPoint(self, side: int, x: int, y: int) -> int:
"""
Map a boundary point (x, y) to a coordinate in [0, 4*side).
- Bottom edge: (x, 0) -> t = x.
- Right edge: (side, y) -> t = side + y.
- Top edge: (x, side) -> t = 3*side - x.
- Left edge: (0, y) -> t = 4*side - y.
"""
if y == 0:
return x
if x == side:
return side + y
if y == side:
return 3 * side - x
return 4 * side - y
def canPlace(self, t: List[int], k: int, side: int, d: int) -> bool:
"""
Given sorted 1D positions 't' (mapped from points) and a candidate distance 'd',
check if we can select 'k' points around the circle (with perimeter L = 4*side)
such that every adjacent gap (in circular order) is at least d.
"""
n = len(t)
L = 4 * side
# Build an "extended" array: ext[i] = t[i] for i in [0, n)
# and ext[i+n] = t[i] + L, to simulate a circular array.
ext = t + [x + L for x in t]
# For each possible starting index in the original array
for i in range(n):
count = 1
pos = ext[i]
idx = i
# Try to pick k points from ext[i+1] up to ext[i+n] (one full circle)
for _ in range(1, k):
target = pos + d
j = bisect_left(ext, target, idx + 1, i + n)
if j == i + n:
count = -1
break
idx = j
pos = ext[idx]
count += 1
# Check the wrap-around gap: from the last chosen point to (first + L)
if count == k and (ext[i] + L - pos) >= d:
return True
return False
def maxDistance(self, side: int, points: List[List[int]], k: int) -> int:
"""
Given the side length 'side' and an array 'points' where each point is [x, y],
return the maximum candidate distance 'd' (in the range [0, 2*side]) such that there
exists a way to select 'k' points (mapped from the given points) around the circle
(with circumference L = 4*side) where every adjacent gap is at least d.
We use binary search over d.
"""
# Map each boundary point to its corresponding 1D coordinate.
t = [self.mapPoint(side, x, y) for x, y in points]
t.sort()
lo, hi, ans = 0, 2 * side, 0
while lo <= hi:
mid = lo + (hi - lo) // 2
if self.canPlace(t, k, side, mid):
ans = mid
lo = mid + 1
else:
hi = mid - 1
return ans